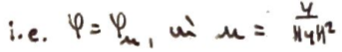Montrer que cette application est surjective :
Montrer que cette application est une isométrie.

On prend \(\varphi\in H^*\) non nulle et on veut montrer qu'il existe \(x\in H\) tq \(\varphi=\varphi_x\).
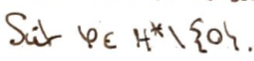
Si \(\varphi\in H^*\) est non nulle, alors son noyau est fermé, convexe et non vide.

On a alors la Projection orthogonale sur \(\ker\varphi\), et on peut définir \(y\) le vecteur correspondant à la différence entre \(x\) et sa projection.
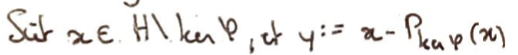
Dans la suite, on suppose \(\varphi(x)=1\) (\(x\notin\ker\varphi\)).
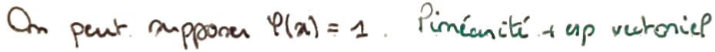
En décomposant, on a alors \(\ker(y)=1\).
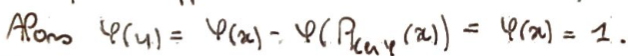
Pour \(z\in H\) quelconque, on a alors \(\varphi(z-\varphi(z)y)=0\).
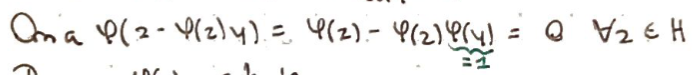
On a alors \(\langle{y,z-\varphi(z)y}\rangle =0\), ce qui se traduit par \(\langle{y,z}\rangle =\varphi(z)\lVert y\rVert^2\).

\(\varphi_u\), avec \(u=\frac y{\lVert y\rVert^2}\) fonctionne donc (on a bien \(\varphi(z)=\langle{u,z}\rangle \)).